Ampere’s Law states that if \(\mathcal{C}\) is a closed curve around a wire that conducts current \(I\), then

\[\int_{\mathcal{C}} {\bf B} \cdot d{\bf r} = kI\]

where \({\bf B}\) is the magnetic field produced by the current \(I\), and \(k\) is a constant.

If the wire is long, thin, and straight, and \(\mathcal{C}\) is a circle centered in the center of the wire and lies in a plane perpendicular to the wire, then the magnetic field \(\bf B\) is tangent to the circle and its magnitude is the same everywhere around the circle. The direction of the magnetic field is determined by the right hand rule.

The magnitude of the magnetic field \(\bf B\) at a distance \(r\) from the center of the wire can be determined by Ampere’s Law.

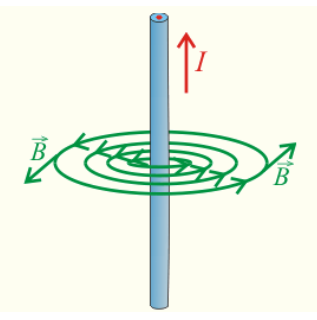
Figure 1: Magnetic field around a straight wire. The wire lies along the z-axis.

In Figure 1, the wire lies along the z-axis, with the current \(I\) flowing along the wire in the positive z direction, represented by \(\hat k\). Using the right-hand rule, we can see that the magnetic field travels counterclockwise around the wire in the xy-plane.

Notice that we integrate over the magnetic field \(\bf B\), and in each step, we consider a small portion of the parametric curve along the magnetic field. Therefore, we need to find a parametrization of the magnetic field.

The magnetic field vector \(\bf B\) is tangent to the curve \(\mathcal{C}\), which encircles the wire. Since the tangent vector \(\bf B\) is parallel to the velocity vector, the angle between these two vectors is \(0^{\circ}\), and \(\cos(0) = 1\). The length of the curve around the wire is \(2\pi\).

To parameterize the curve \(\mathcal{C}\) around the wire, we can use cylindrical coordinates, obtaining

\[\bar{r}(t) = r\cos(t)\hat{i} + r\sin(t)\hat{j} + z \hat{k} \qquad \quad 0 \leq t \leq 2\pi\]

Now we can integrate over this curve. We use the line integral of the tangential component of \(\bf B\) along the curve \(\mathcal{C}\).

—————————————————————————————-

Theorem:

Let \({\bf F}(x,y)\) be a vectorfield and \({\bf r}:[a,b] \rightarrow \mathbb{R}^2\) be a parametrization on the curve \(\mathcal{C}\) and let’s assume that the parametric curve \(\bf r\) is continuously differentiable by sections. The integral of the vectorfield \({\bf F}(x,y)\) along the curve \(\mathcal C\) is defined as

\[\int_{\mathcal C} {\bf F} \cdot d {\bf r} = \int_{\mathcal{C}} {\bf F} \cdot {\bf T} d{\bf s} = \int_a^b {\bf F}({\bf r}(t)) \cdot {\bf r}^{'}(r) \, dt.\]

—————————————————————————————-

The theorem states that

\[\int_{\mathcal{C}}{\bf F} d{\bf r} = \int_{a}^{b} {\bf F}({\bf r}(t)) \cdot {\bf r}^{'}(r) dt\]

Using the theorem, we get

\[\int_{\mathcal{C}}{\bf B} d{\bf r} = \int_{0}^{2\pi} {\bf B}({\bf r}(t)) \cdot {\bf r}^{'}(r) \, dt\]

Looking at the vector \(\bf B\) in figure 1, we see that it is the magnitude \(\vert B \vert\) multiplied by the unit tangent vector \(\bf T\). The equation for the unit tangent vector is

\[{\bf T} = \frac{ {\bf r}^{'}(t) } { \vert {\bf r}^{'}(t) \vert}\]

Thus,

\[{\bf B} = \vert B \vert \cdot {\bf T} = \vert B \vert \cdot \frac{r^{'}(t)}{ \vert r^{'}(t) \vert }\]

We can now write the integral as

\[\int_{\mathcal{C}} {\bf B} \cdot d{\bf r} = \int_0^{2\pi} {\bf B}({\bf r}(t)) \cdot {\bf r}^{'} dt\] \[= \int_0^{2\pi} \vert B \vert \cdot \frac{r^{'}(t)}{\vert r^{'}(t) \vert} \cdot {\bf r}^{'}(t) dt\]

Next, we use the rule \({\bf A}{\bf A} = \vert {\bf A} \vert^2\). This rule can be proofed by using the dot product

\[{\bf A} \cdot {\bf A} = \vert {\bf A} \vert \cdot \vert {\bf A} \vert \cdot \cos(0) = \vert {\bf A} \vert^2\]

Thus, we have

\[\int_{\mathcal{C}} = {\bf B} \cdot d{\bf r} = \vert B \vert \int_0^{2\pi} \frac{ \vert r^{'}(t) \vert^2 }{ \vert r^{'}(t) \vert } dt\] \[= \vert B \vert \int_0^{2\pi} \vert r^{'}(t) \vert dt\]

The length of the velocity vector \(r^{'}(t)\) is

\[\vert r^{'}(t) \vert = \vert - r \sin(t) \hat{i} + r \cos(t) \hat{j} \vert\] \[= \sqrt{(-r\sin(t))^2 + (r\cos(t))^2}\] \[= \sqrt{r^2 \sin^2(t) + r^2 \cos^2(t)}\] \[= \sqrt{r^2} = r\]

Therefore

\[\int_{\mathcal{C}} {\bf B} \cdot d{\bf r} = \vert B \vert r \int_0^{2\pi} dt\] \[= \vert B \vert r \left[ t \right]_0^{2\pi}\] \[= \vert B \vert r 2 \pi\]

Finally, using the Amper’s Law, we get

\[k I = \vert B \vert 2 \pi r\]

Solving for \(\vert B \vert\), the magnitude of the magnetic field is

\[\vert B \vert = \frac{k I}{2 \pi r}\]

Conclusion

The magnitude of the magnetic field around a wire is inversely proportional to the distance from the wire, with the field strength decreasing as the distance from the wire increases.

References

[1] Robert Adams & Christopher Essex. Calculus, A Complete Course, 9th edition.